Limits and continuity are core ideas in calculus that help explain how a function behaves as a variable begins to approach a particular value. Before learning how to find a derivative, students must first understand the definition of a limit and why the limit of a function may or may not exist. These concepts describe whether a function is well-behaved across its domain, whether it becomes infinite, or whether it is discontinuous over an interval.
Using a graph, we can visually define when a function is continuous and explore this important property through simple examples. Platforms like Khan Academy often use this approach to explain key theorems in calculus clearly.
What Is a Limit?
In mathematics, a limit describes what happens to a function as the input x approaches a particular value. The definition of a limit focuses on the behavior of the function near a point, not necessarily the value of the function at a point itself.
A limit exists when the left-hand and right-hand values become equal as x gets closer to that point. If they do not match, the function may show a jump or other types of discontinuity, such as a removable discontinuity. In contrast, polynomial and constant functions usually behave smoothly, meaning the limit exists at every point in its domain.
Limit of a Function Using a Graph
A graph provides a powerful way to understand the limit at a point. Visually, a limit shows how the graph behaves as x approaches the point, even if the function value at that point is missing or different. If you can trace the graph without lifting your pen, it often suggests the function is continuous.
When analyzing a graph, we check the left-hand and right-hand behavior. If both sides approach the same value, the limit of the function exists. However, if the graph shoots upward or downward endlessly, it indicates an infinite limit caused by a vertical asymptote. Gaps in the graph may signal a removable discontinuity, while sudden breaks suggest a jump.
The graph shows a removable discontinuity where the function value differs from the limit, even though the limit exists as x approaches the point.
The graph illustrates a vertical asymptote at x = 0, where the function values increase or decrease without bound. As x approaches the point, the limit becomes infinite, indicating the function is discontinuous.
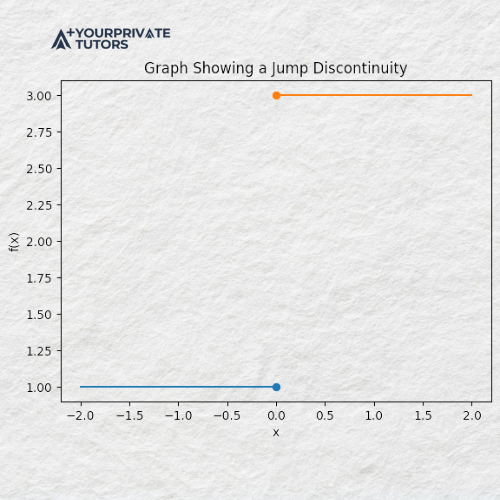
The graph shows a jump discontinuity at x = 0, where the left-hand and right-hand limits approach different values. Since the limit does not exist at this point, the function is discontinuous.
Solved Examples on Limits
Below are three solved examples that show how limits work in different situations. Each example includes a clear explanation and step-by-step solution.
Example 1: Limit of a Constant Function
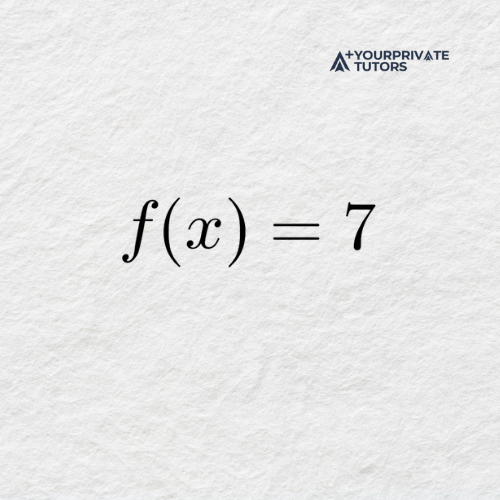
Explanation: Since the function value remains the same, the limit exists and is equal to the constant itself. This is true for all constant functions.
Solution: A constant function has the same value for all values of x. As x approaches any number, the function value does not change.
Example 2: Limit of a Polynomial Function
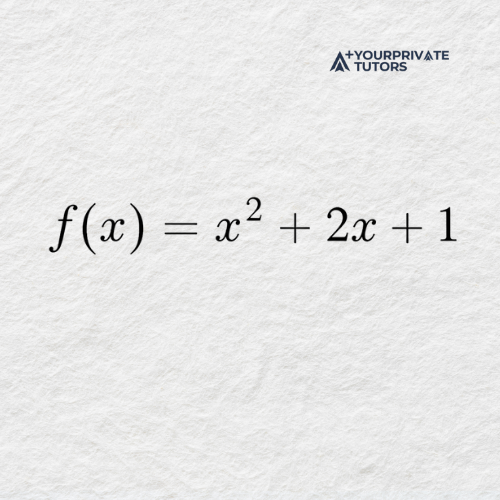
Find the limit as x approaches 1.
Solution: For polynomial functions, the limit can be found by direct substitution.
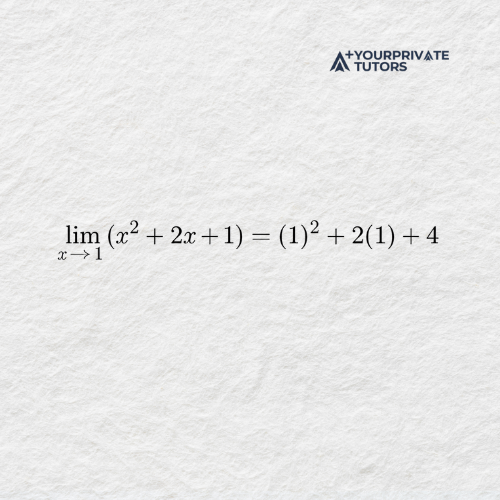
Explanation: Because polynomial functions are continuous, the limit exists and is equal to the value of the function at that point.
What Is Continuity?
The definition of continuity explains how smoothly a function behaves across its domain. In simple terms, continuity refers to a function having no breaks, jumps, or gaps. A function is said to be continuous at a point if the limit at that point exists, the function is defined there, and the function is equal to its limit.
These three conditions must be met for continuity at a particular point. When all conditions are satisfied, the function is continuous at a point. If this happens at every point, the function is considered continuous at every point, which is true for many continuous functions used in calculus.
Understanding the continuity of a function is essential for differentiation and concepts like the intermediate value theorem, which applies only when a function is continuous. Determining whether a function is continuous or discontinuous is also a common topic in exams and frequently asked questions in calculus.
Build the Foundation of Calculus
Learn how limits and continuity work together with clear explanations and visual examples that prepare you for differentiation and beyond.
Conditions for a Function to Be Continuous at a Point
For a function to be continuous at a point, it must satisfy three conditions. These rules help determine whether a function behaves smoothly at a specific location on its graph.
- The function is defined at the point
The function must have a value at that point. If the function at a point is not defined, continuity is impossible. - The limit exists at that point
As x approaches the point from both sides, the function values must approach the same number. If the left-hand and right-hand limits differ, the limit does not exist. - The function value is equal to the limit
The value of the function at the point must match the limit. If these two values are different, the function is not continuous.
When all conditions are satisfied, the function is said to be continuous at a point.
Types of Discontinuity
Not all functions are continuous. When one or more continuity conditions fail, the function becomes discontinuous. The most common types of discontinuity include the following:
Removable Discontinuity
A removable discontinuity occurs when the limit exists at a point, but the function value is missing or different. This appears as a small “hole” in the graph and can often be fixed by redefining the function.
Jump Discontinuity
A jump discontinuity happens when the left-hand and right-hand limits exist but are not equal. The graph suddenly jumps from one value to another, making the function discontinuous at that point.
Infinite Discontinuity
An infinite discontinuity occurs when the function increases or decreases without bound near a point, usually caused by a vertical asymptote. In this case, the limit does not exist, and the graph breaks completely.
Recognizing these discontinuities helps in analyzing limits and continuity accurately.
Intermediate Value Theorem
The Intermediate Value Theorem is an important theorem in calculus that applies to continuous functions. It states that if a function is continuous on a closed interval, then the function takes every value between its values at the endpoints of that interval. In simple terms, if a continuous function starts at one value and ends at another, it must pass through every point in between.
This theorem helps explain why continuity matters in mathematics and calculus, especially when solving equations or locating roots of functions. Because the function has no breaks or jumps, the Intermediate Value Theorem guarantees the existence of certain values within an interval, making it a powerful tool in problem-solving and analysis.
Conclusion
Limits and continuity are essential concepts in calculus that explain how functions behave near specific values and across intervals. Understanding these ideas helps students analyze graphs, evaluate limits, and determine whether functions are continuous or discontinuous.
Mastering this concept is crucial before moving on to differentiation and other advanced topics in mathematics. By practicing with graphs and solved examples, students can build confidence and develop a strong foundation in calculus, making complex problems easier to understand and solve.
If you need extra guidance or personalized support, Your Private Tutor can help you master limits and continuity with clear explanations and one-on-one learning.
