Integration often feels harder than derivatives because instead of applying a clear formula to a function, you’re working backward to figure out which derivative produced it. In derivatives, you follow straightforward rules. In integration, you’re solving a puzzle: given a function in terms of x, what is its original form? That extra layer of thinking is what makes many students pause at each problem.
On this article, we’ll simplify that process. You’ll see a clear listing of common integrals and a helpful table for quick reference.
What Is an Integral in Calculus?
An integral in calculus represents the process of reversing differentiation. In simple terms, if a derivative tells you the rate of change of a function, an integral helps you recover the original function. That original function is called the antiderivative.
When you see notation like
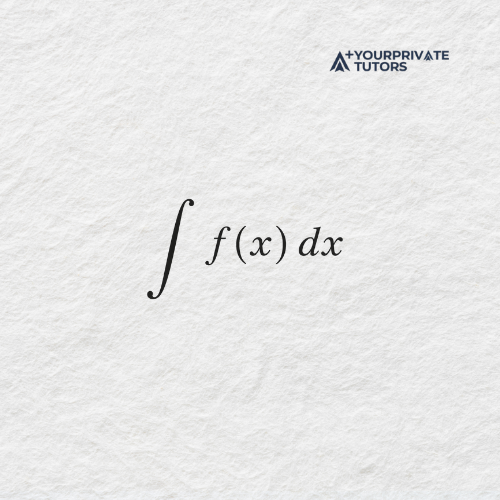
it means you are finding the antiderivative of f(x)f(x)f(x) with respect to xxx. The result of an indefinite integral always includes a constant c, because when you differentiate a constant, it disappears. So multiple functions can share the same derivative, and adding c accounts for that difference.
There are two main types of integrals in calculus:
- Indefinite integrals: These give you a general antiderivative and include + c.
- Definite integral: This calculates a numerical value over an interval, usually representing area under a curve or physical quantities like volume.
The Most Common Integrals You Must Memorize
Success with integration often depends on recognizing patterns quickly. That’s why students rely on a table of integrals, a structured list of the most useful integrals you’ll encounter on exams.
Below is a simplified version of the most standard results you should memorize:
| Function f(x) | Integral | Notes |
|---|---|---|
| xn | xn+1 n+1 + c | Power rule (n ≠ −1) |
| 1/x | ln x + c | x |
| ex | ex + c | Exponential |
| sin x | − cos x + c | Trig |
| cos x | sin x + c | Trig |
These are considered common integrals because they appear repeatedly in AP problems. Many more specific integrals exist especially involving substitution, inverse trig functions, or even infinite series but these core formulas form the foundation.
Mastering this list is the first major step toward confidently solving both indefinite integrals and definite integral problems involving area, volume, or applied calculus situations.
How to Know Which Integration Method to Use
Choosing the right method is the most important skill in integration. While there are many integration rules in mathematics, most AP Calculus problems can be solved by following a simple decision framework. Think of it as a mental checklist you apply every time you see an integral.
Step 1: Can You Use the Power Rule?
If the expression is a basic polynomial like x3, x5 or any simple power of x, start with the power rule. This is one of the most fundamental integral formulas you’ll use.
If the function looks simple and algebraic, try this first. Many students overcomplicate problems that only require straightforward algebra and a direct application of integration rules.
Step 2: Is It a Common Integral from the List?
Next, check whether the function matches something from your table of integrals.
For example:
- 1/x → think ln
- Trig functions like sin x or cos x
- Exponential functions like e^x
Memorizing standard integral formulas saves time and prevents guesswork. Many students keep a printable PDF reference sheet while they study, but for the AP exam, you’ll need these patterns memorized.
The more you study common antiderivatives, the faster your recognition becomes. Over time, your brain connects the function to its antiderivative automatically.
Step 3: Is There a Function Inside Another Function?
If you notice a “function inside a function” pattern like something squared inside parentheses, try substitution.
Substitution works especially well when part of the integrand resembles the derivative of another part. This technique is one of the core integration rules in AP Calculus and builds directly on derivative patterns you already know.
Many online platforms like Khan Academy offer step-by-step video lessons on substitution if you need reinforcement.
Step 4: Is It a Product of Two Functions?
If the integrand is a product (for example, a polynomial times a trig function), consider integration by parts.
Integration by parts comes from a fundamental rule in calculus that relates derivatives and antiderivatives. If substitution doesn’t simplify the expression, and the integrand clearly contains two different types of functions multiplied together, this is often your next move.
Step 5: Is It a Definite Integral Asking for Volume or Area?
If the problem includes limits of integration, you’re dealing with a definite integral. Watch for application wording like “area under the graph” or “volume of a solid.”
After finding the antiderivative, you’ll apply the Fundamental Theorem of Calculus to compute the final value.
When solving applied problems:
- Check if the function is continuous on the interval.
- Confirm you’re interpreting the graph correctly.
- Pay attention to wording related to volume, area, or accumulation.
By consistently applying this five-step framework, you’ll make smarter decisions and avoid random guessing. Keep practicing with web-based exercises, worksheets, and structured study plans to build confidence.
Master Integration for AP Calculus
Learn how integration works with clear explanations, step-by-step examples, and practical strategies that make common integrals, substitution, and the Fundamental Theorem of Calculus easy to understand.
Common Mistakes in AP Calculus Integration
Even strong students lose points on integration because of small but avoidable errors. Here are the most common mistakes and how to prevent them.
1. Forgetting the Constant of Integration
For indefinite integrals, always include the constant of integration (+ c). Since derivatives eliminate constants, every family of antiderivatives differs by a constant.
Forgetting + c is one of the easiest points to lose on exams.
2. Mixing Derivative Rules with Integration Rules
Derivative rules and integration rules are related but they are not identical. For example, students sometimes incorrectly apply power rule steps from differentiation when integrating.
Remember: integration reverses differentiation. Slow down and double-check the correct formula.
3. Not Simplifying Before Integrating
Some problems look complicated but become much easier after basic algebraic simplification.
For example:
- Expand expressions when helpful.
- Break fractions apart.
- Simplify radicals.
Strong algebra skills are essential for success in higher-level mathematics.
4. Misusing ln
A classic mistake is forgetting that the integral of 1/x is ln|x|, not just ln(x). Absolute value matters.
Another error is assuming ln applies to expressions that don’t match the correct derivative pattern. Always verify that the derivative of what’s inside the logarithm appears in the integrand if you’re using substitution.
5. Not Checking Continuity
For definite integrals, make sure the function is continuous over the interval. If there’s a break or discontinuity in the graph, you may need to split the integral into parts.
Ignoring continuity can lead to incorrect values, especially in area and volume problems.
6. Relying Too Much on Online Tools
While online calculators, web solvers, and step-by-step video explanations are helpful for study, they shouldn’t replace understanding.
It’s fine to use:
- Khan Academy practice
- A downloadable PDF of a table of integrals
- Supplementary video lessons
But make sure you understand the reasoning behind the steps not just the final answer.
Final Checklist Before the AP Calculus Exam
Before turning in your exam, mentally run through this checklist for every integration problem:
1. Did I Recognize the Pattern?
- Is it a polynomial (power rule)?
- Is it 1/x (ln rule)?
- Is it exponential or trig?
- Does it require substitution?
2. Did I Apply the Correct Rule?
- Double-check that you didn’t mix derivative rules with integration rules.
- Make sure special cases (like 1/x) were handled properly.
3. Did I Add + c?
- For indefinite integrals, always include the constant of integration.
- For definite integrals, do not include + c.
4. Did I Evaluate Correctly?
- For definite integrals, plug in upper limit minus lower limit.
- Simplify completely.
5. Does My Answer Make Sense?
- If it’s area, should the answer be positive?
- If it’s volume, are the units reasonable?
- Does the result match the structure of an antiderivative?
6. Did I Simplify First?
Sometimes algebraic simplification makes integration much easier.
If you’d like personalized support, guided practice, and expert help tailored to your learning style, consider booking tutoring sessions with Your Private Tutors. Whether you need help reviewing a specific class topic, preparing for the AP exam, or strengthening your calculus foundation, their experienced tutors can guide you step by step.
Sometimes, the fastest way to improve is to learn alongside someone who can explain concepts clearly, answer your questions in real time, and help you minimize mistakes before they become habits.



