If you’ve worked with a matrix before, especially a 2×2, you’ve likely heard about finding its inverse. In linear algebra, the inverse of a matrix undoes the effect of the original when multiplied together. It’s similar to a reciprocal in numbers, but for square matrices and with a few extra steps.
A matrix is only invertible if the determinant is not zero, which makes it a special case. For a 2×2 matrix, you can use a formula involving the determinant and adjugate to calculate the inverse. You’ll swap the diagonal entries, change a few signs, and multiply by one over the determinant. Another way to calculate the inverse is by using row operations such as gauss-jordan or RREF.
Whether you’re solving equations, working with vectors, or exploring a 3×3 matrix, learning how to compute the inverse is a key part of understanding matrix algebra.
What Is the Inverse of a Matrix?
The inverse of a 2×2 matrix, say A, is a matrix of the same order written as A⁻¹, where
A × A⁻¹ = A⁻¹ × A = I. Here, I is the identity matrix of order 2×2:
I = ⎡1 0⎤
⎣0 1⎦
In general, A⁻¹ = adj(A) / det(A), where adj(A) is the adjoint, and det(A) is the determinant.
For a 2×2 matrix:
A = ⎡a b⎤
⎣c d⎦
We use the following formula for the inverse:
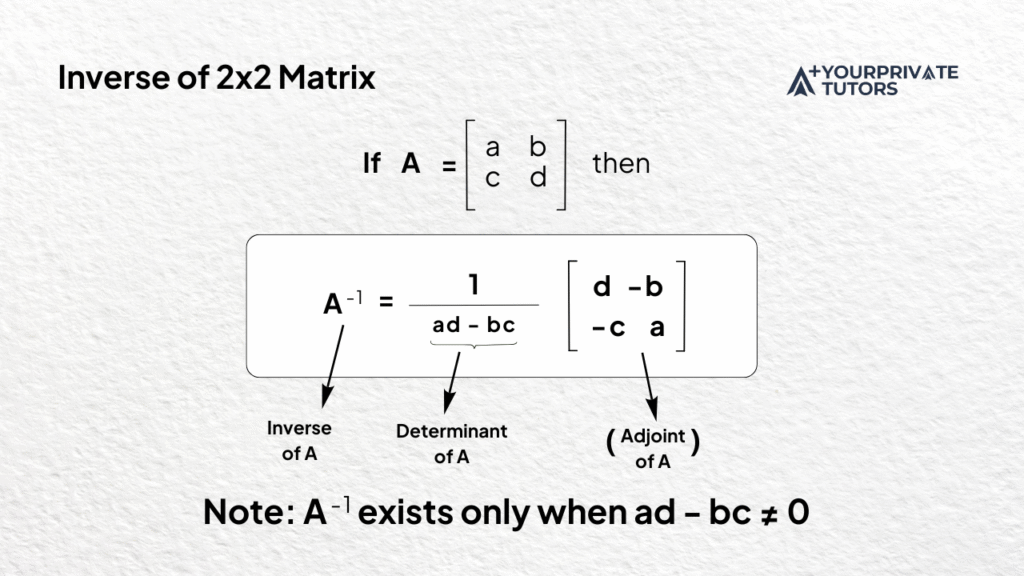
- If ad − bc = 0, A is singular and has no inverse.
- If ad − bc ≠ 0, A is non-singular and invertible.
Next, we’ll look at how to find the determinant and adjugate matrix step by step.
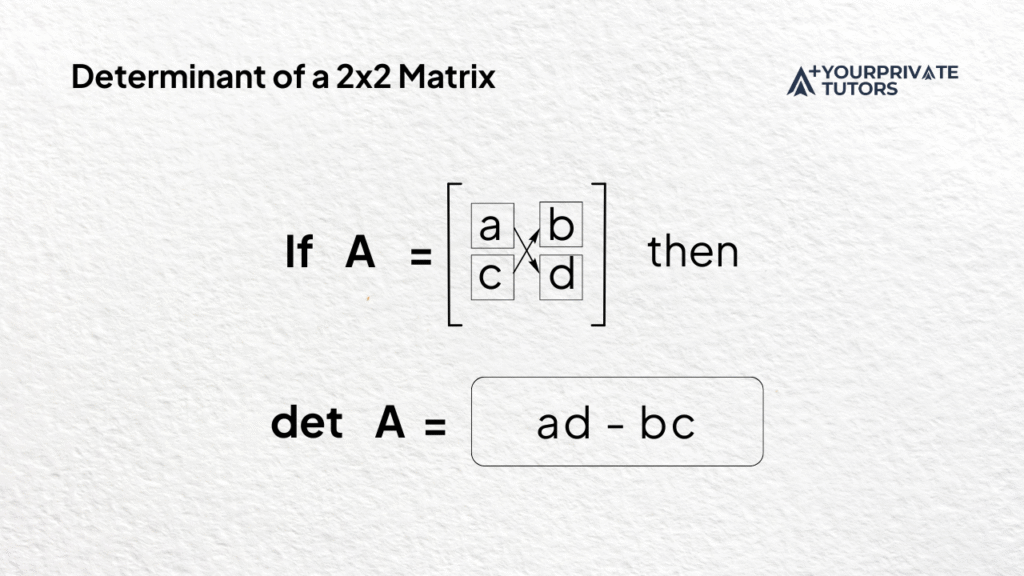
Determinant of a 2×2 Matrix
The inverse of a 2×2 matrix formula uses the determinant of the matrix.
For any matrix A = ⎡a b⎤
⎣c d⎦
The determinant of A is written as:
det(A) = ad − bc
This value is calculated by multiplying the elements of the main diagonal (a and d), then subtracting the product of the off-diagonal (b and c).
This step is crucial—if det(A) = 0, the matrix is non-invertible.
Examples:
The determinant of A = ⎡3 2⎤
⎣1 5⎦
det(A) = (3×5) − (2×1) = 15 − 2 = 13
The determinant of B = ⎡1 2⎤
⎣1 2⎦
det(B) = (1×2) − (2×1) = 2 − 2 = 0
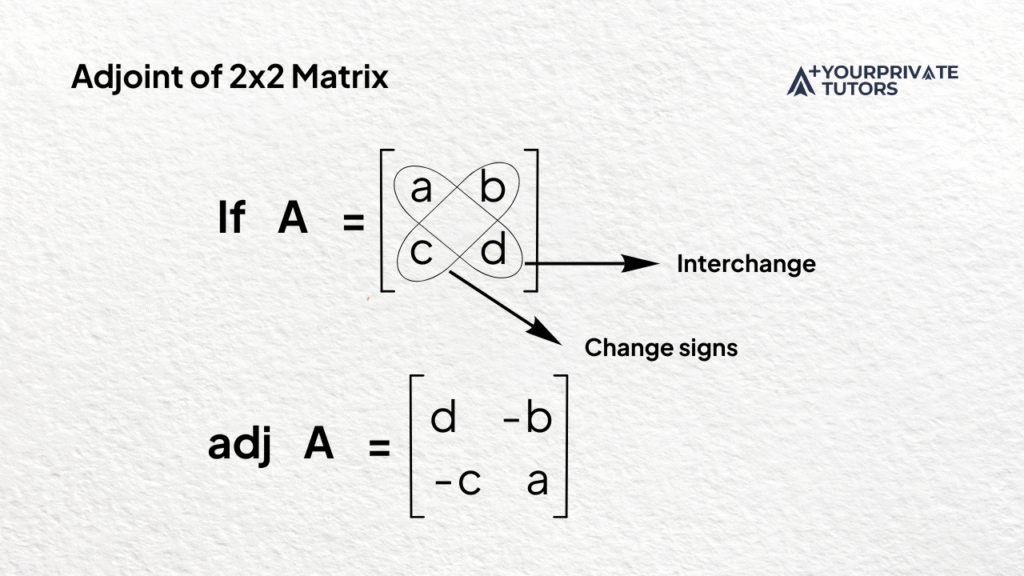
Adjoint of a 2×2 Matrix
The adjoint of a matrix (also called the adjugate) is the transpose of the cofactor matrix.
For a 2×2 matrix, you don’t need cofactors to find the adjoint—just follow this shortcut. For:
A = ⎡a b⎤
⎣c d⎦,
the adjoint of A is:
adj(A) = ⎡d -b⎤
⎣-c a⎦
How to Find the Adjoint:
1. Interchange the elements on the main diagonal (a and d).
2. Change the signs of the off-diagonal elements (b and c).
Example:
If A = ⎡5 -2⎤
⎣-1 3⎦
Then adj (A) = ⎡3 2⎤
⎣1 5⎦
Formula for the Inverse of a 2×2 Matrix
Matrices are powerful tools in linear algebra. Learning how to find the inverse of a 2×2 matrix helps solve systems, simplify equations, and understand transformations with clarity.
For a given matrix A = ⎡a b⎤
⎣c d⎦
the inverse matrix is:
A⁻¹ = (1 / (ad − bc)) × ⎡d −b⎤
⎣−c a⎦
Here, ad − bc is the determinant, and the inverse exists only when this determinant is non-zero. If det(A) = 0, the matrix is not invertible.
Breaking Down the Formula:
- The determinant is calculated as ad − bc, the difference of the diagonal products.
- To form the adjoint, swap the diagonal entries a and d, then change the signs of b and c. This process is sometimes called “diagonal and changing.”
- Multiply the adjoint by 1 / (ad − bc) to get the final inverse.
This multiplicative property ensures that when the inverse of matrix A is found, it can be multiplied by the original matrix to give the identity matrix.
Although we can also use elementary row operations, an augmented matrix, or methods like Gaussian elimination or LU decomposition for larger 3×3 cases, this formula is the fastest way to compute the inverse of a 2 × 2 matrix. It is widely used in matrix multiplication, solving a system of equations using matrices, and in more advanced matrix inversion with complex numbers or decomposition.
Step-by-Step with a 2×2 Matrix Using the Formula
Consider the matrix A = ⎡a b⎤
⎣c d⎦
Step 1: Calculate det(A)
det(A) = ad − bc = (2 × 4) − (3 × 1) = 8 − 3 = 5.
Since ad − bc ≠ 0, A is part of the family of invertible matrices.
Step 2: Apply the formula
Using the formula for the inverse matrix:
A⁻¹ = (1 / det(A)) × ⎡d −b⎤
⎣−c a⎦
Step 3: Substitute values
A⁻¹ = (1 / 5) × ⎡4 −3⎤
⎣−1 2⎦
Here, we invert the diagonal entries (swap a and d) and change the signs of the other two. This step is often called diagonal and changing.
Step 4: Simplify
A⁻¹ = ⎡4/5 −3/5⎤
⎣−1/5 2/5⎦
Finding the Inverse Matrix Using Elementary Row Operations
The inverse of a 2×2 matrix can also be found using elementary row operations. Begin with an augmented matrix:
⎡a b | 1 0⎤
⎣c d | 0 1⎦
Apply row operations such as swapping, scaling, or adding rows until the left side becomes the identity matrix. The right side then gives A⁻¹. This method is closely related to solving systems of equations and is a practical way to understand matrix inversion. It can also be extended to larger 3×3 matrices.
Solving System of 2×2 Equations Using Inverse
We can solve a system of equations neatly by using the inverse of a matrix.
Example:
2x + y = 5
3x − 5y = −7
Step 1: Write the system in matrix form AX = B
This expresses the equations compactly with a matrix containing coefficients.
A = ⎡2 1⎤ X = ⎡x⎤ B = ⎡5⎤
⎣3 −5⎦ ⎣y⎦ ⎣−7⎦
Step 2: Find the determinant and the inverse of A
Check if A is invertible by calculating det(A) = ad − bc.
det(A) = (2 × −5) − (1 × 3) = −13
A⁻¹ = (1 / −13) × ⎡−5 −1⎤
⎣−3 2⎦
Step 3: Solve using the inverse
Multiply A⁻¹ by B to isolate X.
X = A⁻¹B = ⎡ 1 ⎤
⎣ 2 ⎦
So x = 1 and y = 2.
Here, using the inverse allows us to get the identity matrix on the left, leaving X alone. The process always works for invertible matrices and can extend to larger systems, such as a 3×3 matrix.
Common Mistakes When Finding an Inverse
When learning to find the inverse of a 2×2 matrix, a few errors come up often. These usually happen when applying the formula or when checking the result. Keeping these in mind can save time and confusion:
- Not checking if ad − bc ≠ 0. A zero value means the matrix has no inverse.
- Swapping or changing the wrong entries in the formula.
- Assuming multiplication is commutative with another matrix; this only holds for A × A⁻¹.
- Forgetting to test by multiplying with A or with matrix B to confirm you get the identity matrix.
Practice Makes Perfect with Matrix Inversion
The inverse of a 2×2 matrix is a key concept in linear algebra. We reviewed its definition, the condition ad − bc ≠ 0, the formula, examples, and applications such as solving systems. The method becomes easier with practice, especially when you swap entries, change signs, and verify results by multiplication.
The best way to improve is to keep testing with different matrices and confirm that A × A⁻¹ gives the identity. As your next step, challenge yourself with the inverse of a 3×3 matrix, and remember we are here to help you aim for clarity, confidence, and betterment.






