In physics and mathematics, many quantities cannot be fully described by a single number alone. Direction often matters just as much as size, especially when dealing with motion, forces, or displacement. This is where vectors come in.
Before learning how to combine vectors using methods like the tip-to-tail approach, it’s important to understand what a vector is and why vector addition plays such a crucial role.
Using a graph, we can visually define when a function is continuous and explore this important property through simple examples. Platforms like Khan Academy often use this approach to explain key theorems in calculus clearly.
What Is a Vector and Why Vector Addition Matters
A vector is a quantity that has both magnitude and direction, which sets it apart from a scalar. Scalars, such as mass or temperature, are described by magnitude only. In contrast, vector quantities like velocity, displacement, and force require both how large the quantity is and the direction of a vector to be fully defined.
Vector addition is fundamental in physics and engineering because real-world problems rarely involve just one vector acting alone. Whether calculating net force, total displacement, or combined velocity, understanding vectors and how their magnitudes and directions interact is essential for solving problems accurately.
What Is the Tip-to-Tail (Head-to-Tail) Method of Vector Addition
The tip-to-tail method, also known as the head-to-tail method, is a graphical technique used to add vectors by arranging them in a specific order. In this method of vector addition, vectors are added by placing them end to end so their directions are preserved. This approach visually shows how vectors combine and makes it easier to understand the direction of the vector that results from the addition.
The core rule is simple: place the tail of the second vector at the head of the first vector. When working with vectors A and B, vector B is moved (without changing its length or direction) so that its tail touches the head of vector A. The vectors themselves are not altered, only their position is changed. This rule applies not only when adding two vectors but also when adding two or more vectors in sequence.
How to Add Two Vectors Graphically Using the Tip-to-Tail Method
To add two vectors using the tip-to-tail method, follow this graphical, step-by-step process. This approach helps visualize how vectors combine to form a single resultant vector.
Step 1: Draw the first vector
Draw the first vector to scale using a ruler. The length of the arrow represents its magnitude, and the arrowhead shows the direction of the vector. For example, the vector may point due east or eastward, depending on the problem.
Step 2: Place the tail of the second vector correctly
Take the second vector (often labeled vector B) and place the tail of the second vector at the head of the first vector. The tail of the first vector remains fixed. Only the position of vector B changes, not its length or direction.
Step 3: Maintain the original direction of each vector
When working with vectors A and B, ensure both vectors keep their original orientations. This step is essential in vector operations, since changing direction would change the sum of the two vectors.
Step 4: Draw the resultant vector
Draw the resultant vector, labeled vector r, from the tail of the first vector to the head of the last vector. This arrow represents the vector sum of the two vectors.
Step 5: Determine the magnitude of the resultant
If the vectors are perpendicular or form a right angle, they create a right triangle. In this case, you can determine the magnitude of the resultant by applying geometry and use the Pythagorean theorem to calculate the length of the hypotenuse.
Step 6: Find the direction of the resultant vector
Measure the angle of vector r using a protractor, or calculate it mathematically using the vector addition formula. This gives the final direction of the vector relative to a reference direction.
Master Vector Addition Step by Step
Learn how limits and continuity work together with clear explanations and visual examples that prepare you for differentiation and beyond.
Vector Components and the Coordinate (Cartesian) Method
While the tip-to-tail method works well graphically, many vector problems especially those involving angles are easier to solve using vector components and the coordinate (Cartesian) method. This approach is especially useful for vectors in two dimensions, where motion or forces act along both vertical and horizontal directions.
In this method, vectors are broken down into their x- and y-components using a coordinate system. Each vector is resolved into a horizontal component along the x-axis and a vertical component along the vertical axis. This allows vectors to be handled algebraically, making addition and subtraction more systematic and precise.
Adding Three or Four Vectors Using Tip-to-Tail
The tip-to-tail method is not limited to just two vectors, it works just as effectively when adding three vectors or even four vectors. The process remains the same: vectors are arranged head to tail, one after another, while preserving their original magnitudes and directions.
To add multiple vectors, start by drawing the first vector drawn from the tail to scale. The second vector is then placed head to tail with the first, followed by the third, and so on. Each vector must be drawn to scale using consistent units using the scale so that the final result is accurate. This sequential arrangement visually shows how vectors add together, regardless of how many are involved.
Practice Problems
The following practice problems apply the tip-to-tail method, vector components, and basic trigonometry to common vector scenarios. Work through each problem step by step to strengthen your understanding of vector addition and subtraction.
Practice Problem 1: Adding Two Perpendicular Vectors
Problem: A displacement of 6 meters occurs due east, followed by a displacement of 8 meters due north. Find the magnitude and direction of the resultant vector.
Solution:
- Draw the first vector due east, then place the second vector head to tail pointing north.
- The two vectors are perpendicular, forming a right triangle.
- The resultant vector r is the hypotenuse of the triangle.
To find the magnitude and direction (respectively):


This gives an angle of approximately 53° north of east.
Answer: The resultant displacement is 10 meters at 53° north of east.
Practice Problem 2: Vector Components Method
Problem: A force vector of 50 N acts at an angle of 30° above the horizontal. Determine its horizontal and vertical components.
Solution:
- Use trigonometric functions to resolve the vector.
- Horizontal and Vertical Component (respectively)
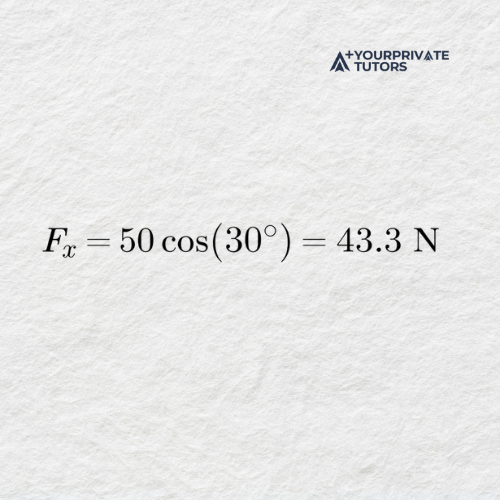
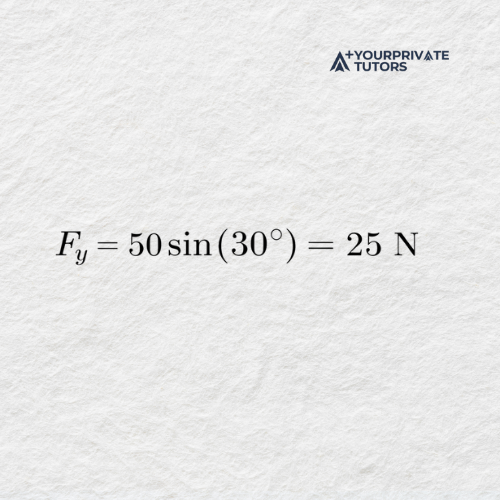
Answer: The force has a horizontal component of 43.3 N and a vertical component of 25 N.
Conclusion
The tip-to-tail method is a simple and effective way to add and subtract vectors, helping visualize how displacement and force vectors combine. By placing vectors head to tail, the sum of two vectors can be found regardless of their order, with the resultant’s magnitude and direction determined using geometry or trigonometry.
When vectors form a right triangle, the length of the resultant can be calculated using the Pythagorean theorem, while angles are measured using sine and cosine. These concepts apply to real-world problems such as motion and free-body diagrams. For additional support and clearer explanations, Your Private Tutor provides helpful guidance in mastering vector concepts.



