Trigonometry is a vital branch of mathematics that explores the relationships between an angle and the sides of a triangle. At its core, it studies how measurements of angles connect to specific number patterns called trigonometric ratios.
In a basic right triangle, the sine, cosine, and tangent describe these relationships as a ratio between the hypotenuse and the other sides. Over time, these ratios developed into full trigonometric functions, each with its own formula and powerful identity.
In pre-calculus, students move beyond triangles and discover the unit circle, a tool that redefines every trigonometric function in a simpler and more unified way.
By understanding this shift, you’ll see how sine, cosine, tangent, and their related functions all connect through clear patterns and fundamental trigonometric identities. In the next section, we’ll build that foundation step by step.
Step 1: From Right Triangle Trigonometry to the Unit Circle
To understand the unit circle, we first review the basics of right triangle trigonometry. A right triangle contains one 90-degree angle, and the side opposite that angle is called the hypotenuse. The other two sides are labeled adjacent and opposite, depending on the chosen angle.
The three main trigonometric ratios are defined using these sides. The sine function is the ratio of the opposite side to the hypotenuse. The cosine function (often written as cos) is the ratio of the adjacent side to the hypotenuse. The tangent function compares the opposite side to the adjacent side. Each ratio can be written as a clear formula, helping us calculate unknown sides or angles in a triangle.
Beyond these three, there are reciprocal functions: cosecant, secant, and cotangent, which are derived from sine, cosine, and tangent. Together, they form the foundation of many important trigonometric identities used throughout mathematics.
Step 2: What Is the Unit Circle in Trigonometry?
The unit circle is a circle with a radius of 1 centered at the origin (0,0) on a coordinate plane. It’s called “unit” because its radius is exactly one unit long. While trigonometry often begins with a right-angled triangle, the unit circle allows us to move beyond the limits of the sides of triangles and define trig relationships for any angle.
Angle measurement starts at 0° on the positive x-axis and moves counterclockwise. If we label an angle as θ (theta), the point where its terminal side meets the circle has coordinates (cos θ, sin θ). This means sine and cosine are no longer just trigonometric ratios such as sine defined by the length of the hypotenuse and other sides.
This shift is powerful. In a triangle, we use ratios to compute unknown sides or find the missing angles. But in the unit circle, the relationships between angles and sides become part of a bigger system that shows how the functions relate across all angle measures, including those greater than 90° or even 360°.
Step 3: Understanding Sine, Cosine, and Tangent as Functions
In a right-angled triangle, sine, cosine, and tangent are defined using the three sides. For example, sine equals the opposite side divided by the length of the hypotenuse, and cosine equals the adjacent side divided by the hypotenuse. These definitions focus on the angles and sides of triangles.
However, in the unit circle, these ratios become full trigonometry functions. Instead of depending on the physical sides of triangles, sine and cosine are defined by coordinates. For any angle θ, cos θ represents the x-coordinate, and sin θ represents the y-coordinate of the point on the circle. This allows us to work with angles of any size and simplifies computation.
The tangent function is defined as:
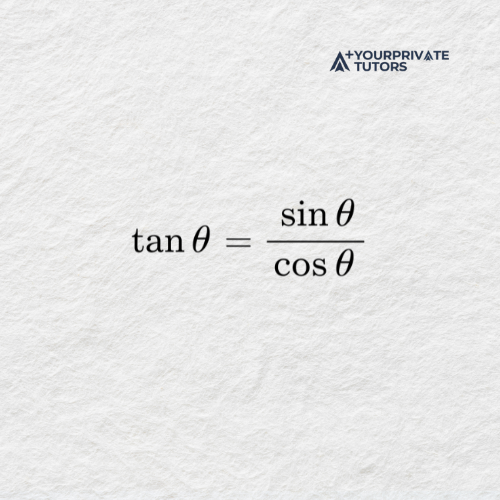
This formula shows how the functions relate to each other. Because of this relationship, many identities and shortcuts commonly used in trigonometry become easier to understand.
We also define reciprocal trig functions:
- Secant = 1 / cosine
- Cosecant = 1 / sine
- Cotangent = 1 / tangent
Together, these six trig functions describe consistent relationships between angles and sides, even when no triangle is drawn.
Master Integration for AP Calculus
Learn how the unit circle works with clear explanations, step-by-step guidance, and practical strategies that make sine, cosine, tangent, formulas, and identities easier to understand.
Step 4: Key Identities and the Core Formula to Remember
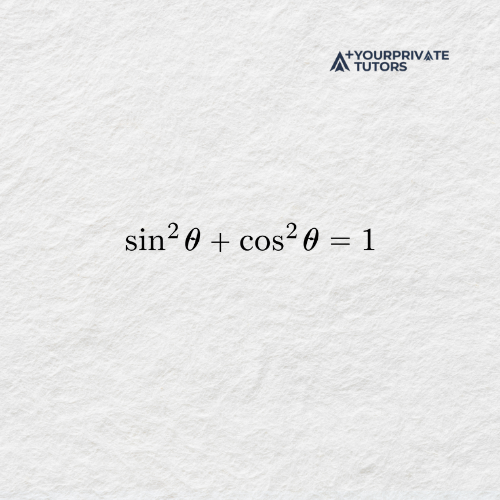
This formula comes directly from the Pythagorean Theorem. In a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. When that triangle is placed inside the unit circle (where the hypotenuse equals 1), the relationship naturally becomes this identity. It shows how the relationships between the angles and the coordinates on the circle always stay consistent.
Earlier, you may have learned SOHCAHTOA, which connects the three basic trig ratios to the sides and angles of a triangle. That memory tool still applies, but now the identity shows how sine and cosine are mathematically linked. These core relationships help us solve for unknown angles or missing side lengths using inverse trig functions.
For example, if we know the sine of an angle, we can use the inverse sine function to find the angle formed in a triangle. If we know one side of a triangle and another measurement, trigonometric functions are used to determine the remaining values. These identities simplify complex problems in algebra and higher mathematics because they reveal predictable patterns in trigonometry angles.
Understanding this formula strengthens your overall knowledge of trigonometry and prepares you to work confidently with more advanced identities and equations.
Step 5: Applications of Trigonometry Beyond the Classroom
The applications of trigonometry stretch far beyond textbook exercises. In fact, the history of trigonometry shows that it developed from real-world needs. Ancient civilizations such as the Babylonian culture and scholars in Alexandria studied angles and measurements to track the stars. Later, astronomers like Ptolemy advanced trigonometric tables to improve calculations in astronomy.
In astronomy and navigation, spherical trigonometry is used to measure angles and distances across curved surfaces like Earth or the sky. Trigonometric functions are used to calculate planetary motion, star positions, and satellite paths.
In the physical sciences, trigonometry plays a major role in physics, engineering, and optics. For example, when analyzing an angle of elevation, such as measuring the height of a building from a certain distance, we use the angle formed between the ground and the line of sight. With one side of a triangle known and a right angle creating a perpendicular structure, trig ratios help us compute the missing height.
Conclusion
Trigonometry is far more than just solving a triangle or memorizing a simple ratio. As you’ve seen, the unit circle brings every trigonometric idea together, connecting sine, cosine, tangent, and their identities into one unified system. Instead of focusing only on the sides of a triangle, you now understand how these functions work for any angle and how they support deeper concepts in algebra and beyond.
By mastering these five steps, pre-calculus becomes much more manageable. The patterns become clearer, the formulas feel more logical, and graphing trig functions starts to make sense.
If you’d like extra guidance while building confidence with these concepts, working with an experienced tutor can make a big difference. Your Private Tutors offers personalized support to help you strengthen your understanding and succeed in trigonometry and beyond.



